Algoritmos y sus complejidades
Tengo que buscar algo en una lista de 300,000 registros, pero mi algoritmo de búsqueda tarda demasiado ¡Ayuda!
Si eres programador, sabrás que unos algoritmos pueden ser más rápidos que otros a la ahora de obtener el mismo resultado, pero esto no es solo porque la computadora tenga un procesador más rápido o más memoria, cada algoritmo que hagamos tiene cierta complejidad que influye directamente en el tiempo que tomará para ejecutarse, dependiendo de la cantidad de datos que use. Es decir, un algoritmo con una complejidad más alta tomará más tiempo en ejecutarse que un algoritmo con una complejidad más baja.

Esta misma complejidad respecto al tiempo, se puede trasladar a la memoria usada por el mismo algoritmo, no es lo mismo hacer una búsqueda lineal en una lista de 300,000 datos desordenada a hacer una búsqueda binaria en una lista previamente ordenada, en el primer caso, necesitamos cargar todos los datos en memoria, mientras en el segundo podemos cargar en memoria solo el segmento de la lista que nos interesa.
Notación de la O grande (Big O)
Esta notación nos sirve para describir la complejidad en cuanto a tiempo, o memoria, del algoritmo que queremos analizar.
Si lo queremos ver matemáticamente respecto al tiempo, una notación theta acota asintóticamente el crecimiento del tiempo de ejecución dentro de un máximo o un mínimo. Es decir, teniendo un algoritmo de búsqueda lineal con n datos, puede ser que el dato que estemos buscando este en la primera posición o en la última, es decir el tiempo de ejecución puede ser θ(1) en el mejor de los casos o en el peor de los casos θ(n). Esta última seria nuestra O grande.
En términos más sencillos, la notación de la O grande describe el tiempo máximo de ejecución que necesita nuestro algoritmo para completarse, tomando en cuenta la cantidad de datos ‘n’ o cantidad de operaciones que se tienen que ejecutar. Puede que tome menos tiempo, pero nunca sobrepasará ese límite dado por O grande.
Clasificación de algoritmos
Cada algoritmo tiene su propio valor de O, pero para evitar calcular esto cada vez, existen clasificaciones que nos facilitan evaluar el algoritmo más rápidamente.
| Big O | Descripción |
|---|---|
| O(1) | Tiempo de ejecución constante. No importar la cantidad de datos, es el valor ideal de cualquier algoritmo, pero raramente alcanzable. |
| O(log n) | Algoritmo logarítmico. El tiempo de ejecución crece logarítmicamente en proporción a n. Por ejemplo, la búsqueda binaria. |
| O(n) | Algoritmo lineal. El tiempo de ejecución crece linealmente respecto a n, como lo es con una búsqueda lineal. |
| O(n * log n) | Algoritmo super-logarítmico. El tiempo de ejecución crece en cierta proporción respecto a n. Por ejemplo, merge sort . |
| O (n^c) | Algoritmo polinomial. El tiempo crece exponencialmente, como puede ser un algoritmo de burbuja. |
| O(c^n) | Algoritmo exponencial. El tiempo de ejecución crece exponencialmente respecto a n. como puede ser la solución de la torre de hanoi. |
| O(n!) | Algoritmo factorial. El tiempo de ejecución crece rápidamente respecto a n. Este es el peor tipo de algoritmos ya que se hace inútil rápidamente a medida que n crece. Un ejemplo de esto sería la búsqueda por fuerza bruta del algoritmo del viajero. |
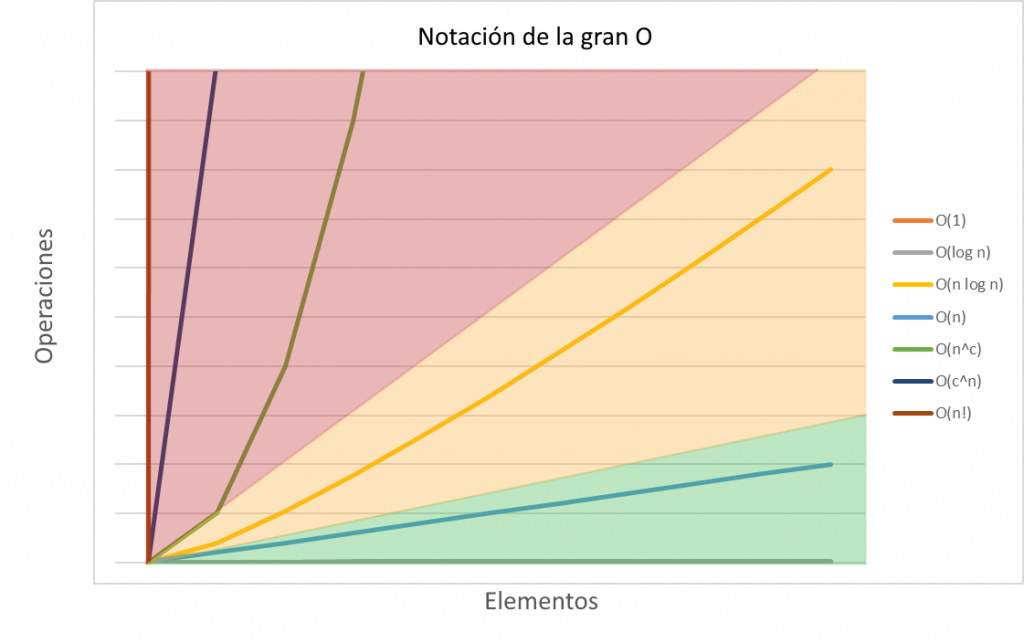
En resumen, la notación de la gran O es importante para medir la eficiencia de nuestros algoritmos, sobre todo si vamos a manejar una gran cantidad de datos o tenemos un poder limitado de procesamiento o de memoria. Entre más eficiencia necesitemos, más nos tenemos que acerca al menos a una complejidad de O(log n).